Hello Friends,
I hope you are doing well. In our previous articles, we have learned about what is stress, strain, types of stress and strain etc. In this article, we are going to discuss about the stress-strain relationship and also learn about the stress-strain curve which is very important to predict any material behavior when it is subjected to load.
Let’s start with its definitions.
Stress is developed in an object when it is subjected to load. Mathematically it is the ratio of applied load to the cross-section area of the body. It is shown by σ and its unit is N/m2.
Strain is the measurement of deformation induced in the object when it is subjected to the load or stress. Mathematically it is equal to the ratio of change in dimension to original dimension. It is a unitless quantity and shown by ϵ.
Stress-Strain Curve:
This curve represents the behavior of any material or object during the loading condition. It is used to predict safe loading conditions, failure point, fracture point etc. This diagram is very useful in the design of any machine.
To plot this diagram, stress is plotted along the vertical axis and strain is plotted on the horizontal axis. A specified dimension object and a universal loading machine are used to perform this experiment. An increasing load is applied by a universal loading machine on the object which induced stress as well as the strain in the object. For every load, we get a different stress and strain value which is plotted on a graph with the help of a specially designed computer. As we increase the load, we get a point where the object breaks into two parts. This is called fracture or failure point. We plot the curve at the end of this point.
The stress-strain curve is different for ductile and brittle material. For ductile material, it is given below.
Explanation of various point of stress-strain curve for ductile material:
Proportional Limit:
As the name implies, in this region of the stress-strain curve, stress is directly proportional to strain. The ratio of stress to strain gives always a similar constant within this limit. This constant is known as the Young Modulus of Elasticity. It is shown by AB in the diagram. The object gets its initial dimension after the load is removed within the proportional limit.
Elastic Limit:
This limit is shown by AC in the diagram. This limit is a slighter upgrade version of proportional limit. It is a combination of proportional limit AB and a slighter increase part BC in which stress is not directly proportional to the strain. It is called the elastic limit because the object gets its initial dimensions when the load is removed. If we increase the load or stress beyond this limit, the object will not get its original dimensions ever at its own.
Yield Point:
When we increase the load beyond the point C, the object starts to deform permanently or it will never get back its initial dimensions. If we increase the load or stress continuously we reach a point where the stress-strain curve changes its slop and start to move in the negative direction. This point is shown by D. The upper point at which it reaches without changing its slop is known as upper yield point. Beyond the upper yield point, the object continuously and rapidly changes its dimension without changing the loading condition or decreasing the loading condition or stress. After reaching the upper yield point there is no option to stop the deformation. The object continuously deforms until it reaches another point which is called the lower yield point. It is shown by the letter E in the curve. If we lower down the loading below the lower yield point, the continuous deformation will stop.
Ultimate stress point:
If we continuously increase the load or stress on the object after reaching lower yield point, the strain or deformation in the object also increases. After a continuous loading, we reach a point after which it is impossible to get back the object without fracture or failure. This point is known as the ultimate stress point. It is shown by F. The strain in the object continuously increases after this point without increasing the loading as well as after decrease the loading. All the engineering application works under a safe limit which is calculated by this point.
Breaking point or fracture point:
After the ultimate stress point, there is no option to get back the object without fracture. The point in the curve at which the object will fail or fractured is known as fracture or breaking point. It is shown by G in the curve.
This is all about the stress-strain curve. If you have any query regarding this article, ask by commenting. If you like this article, don’t forget to share it with your friends. Subscribe our website for more informative articles. Thanks for reading it.
Stress Strain Curve : Full Explanation
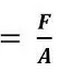 Reviewed by Admin
on
July 28, 2018
Rating:
Reviewed by Admin
on
July 28, 2018
Rating:
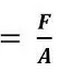 Reviewed by Admin
on
July 28, 2018
Rating:
Reviewed by Admin
on
July 28, 2018
Rating:







No comments: